
Conceitos Iniciais em Grafos
Ludmila Maciel Rocha de Souza

Porque estudar grafos ?
- Arcabouço matemático com aplicação em diversas áreas do conhecimento;
- Utilizados na definição e/ou resolução de problemas;
- Estudar grafos é mais uma forma de solucionar problemas computáveis;
- Os estudos teóricos em grafos buscam o desenvolvimento de algoritmos mais eficientes;
- Abstração matemática que representa situações reais através de um diagrama.
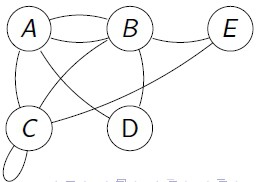
Conceito de grafo
Grafo G = (V, E)
-> V é o conjunto de vértices (bolinhas).
-> E é conjunto de arestas, que são relações entre os vértices.
Exemplo:
Classificação
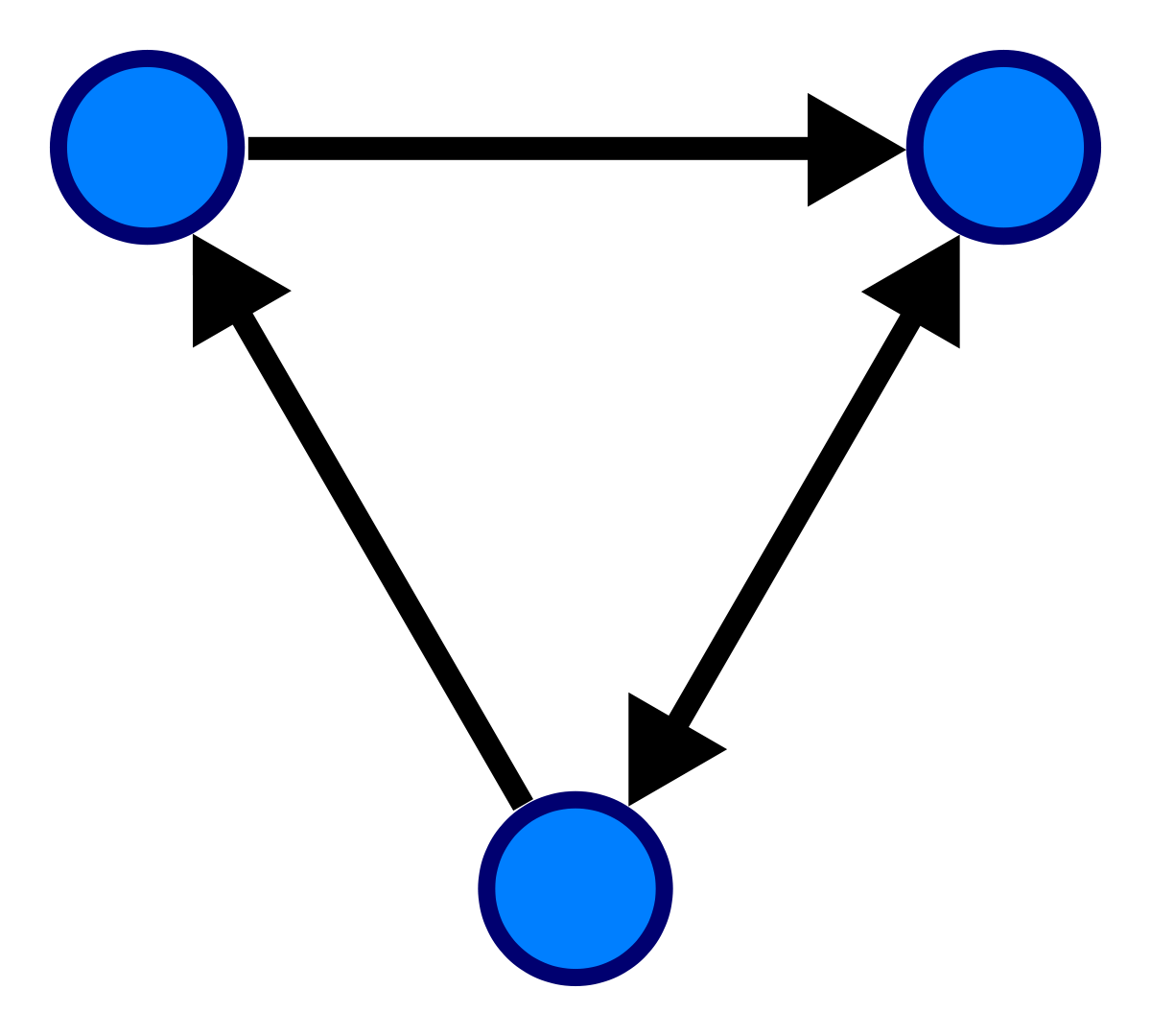
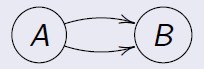
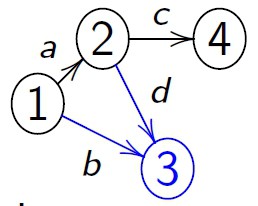
-> Direcionado (Orientado / Dígrafo): Par G = (V,E), onde V é um conjunto finito e E é uma
relação binária em V.
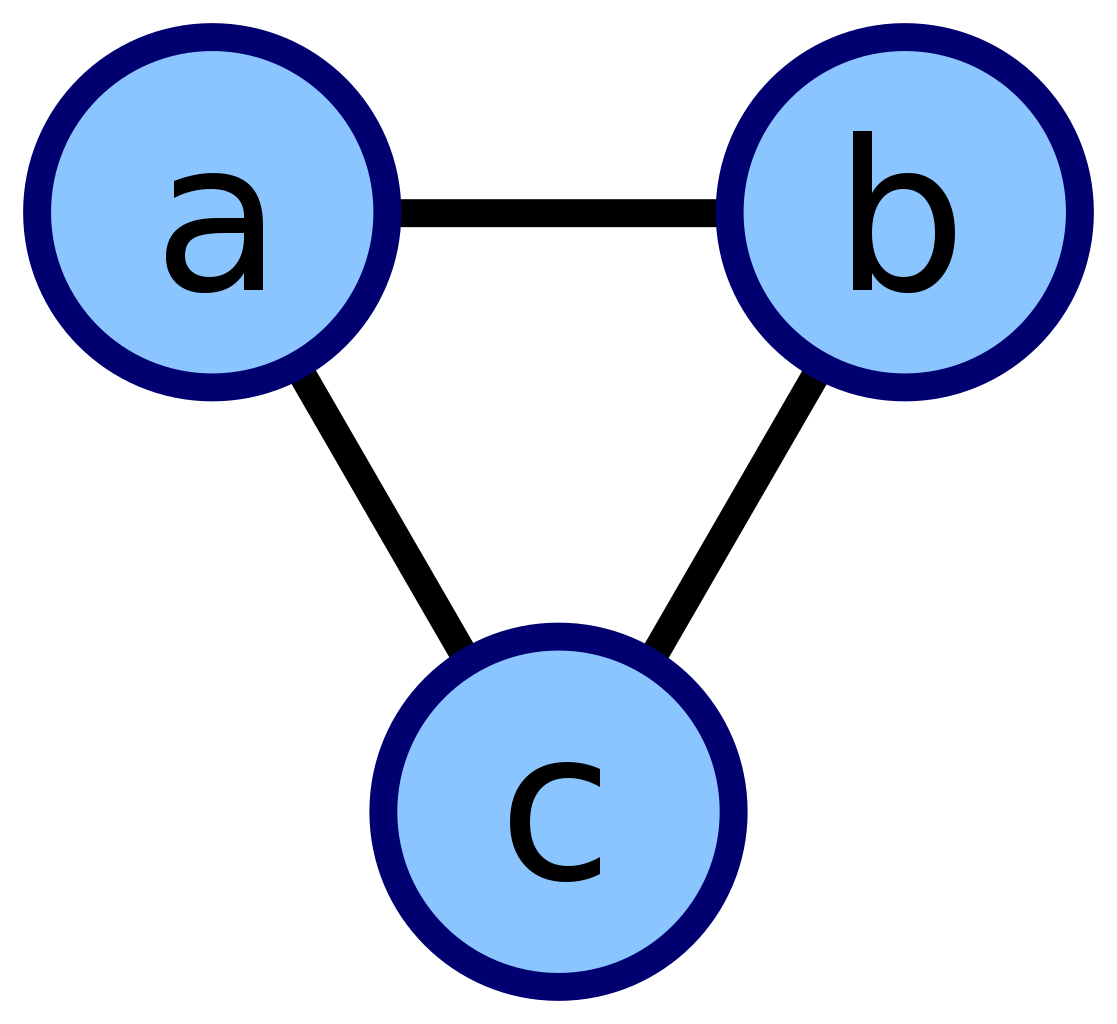
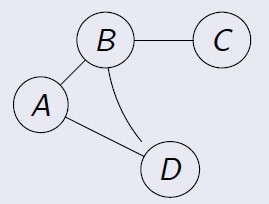
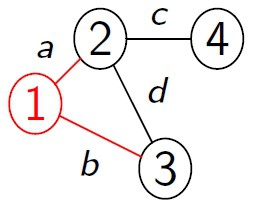
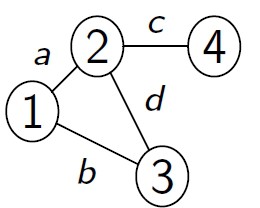
-> Não Direcionado (Não Orientado): Par G = (V,E) onde o conjunto de arestas E consiste em pares
de vértices não orientados. A aresta (vi ; vj ) e (vj ; vi ) são consideradas a mesma aresta.
mais terminologias
-> Loop: uma aresta associada ao par de vértices (vi ; vi ).
-> Arestas Paralelas: quando mais de uma aresta está associada ao mesmo par de vértices.
-> Grafo Simples: um grafo que não possui loops e nem arestas paralelas.
-> Vértices adjacentes: dois vértices são ditos adjacentes se eles são pontos finais de uma mesma aresta.
grau de um vértice
-> Grafo não direcionado:
- grau d(v) - número de arestas que incidem em v.
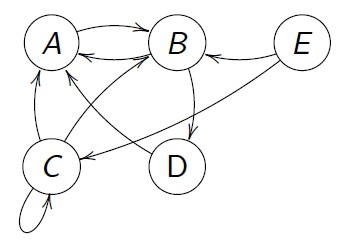
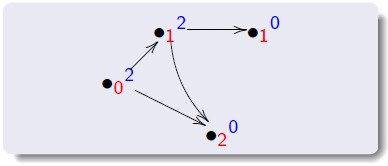
-> Grafo direcionado:
- grau de entrada d-(v) - número de arestas que chegam em v.
- grau de saída d+(v) - número de arestas que saem em v.
-> Observação:
- Um laço conta duas vezes para o grau de um vértice.
-> Exemplos:
mais terminologias
-> Duas arestas não paralelas são adjacentes se elas são incidentes a um vértice comum
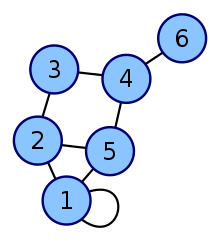
-> Quando um vértice vi é o vértice final de alguma aresta ej, vi e ej são incidentes, ou seja, os dois vértices ligados por uma aresta são ditos suas extremidades e a aresta é dita que é incidente para com os vértices.
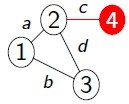
Nas figuras abaixo, por exemplo, um vértice vi pode ser representado pelo vértice de número '2', enquanto que uma aresta ej pode ser representada pela aresta 'a'. Sendo assim, o vértice '2' é o vértice final da aresta 'a', indicando que 'a' incide em '2'.
-> Sequência de graus: consiste em escrever em ordem crescente o grau de todos os vértices de um grafo.
-> Vértice isolado: um vértice com nenhuma aresta incidente.
-> Vértice pendente: vértice com grau 1.
mais terminologias
->Grafo nulo: um grafo sem nenhuma aresta. Todos os vértices em um grafo nulo são vértices isolados.
-> Grafo regular: um grafo no qual todos os vértices possuem o mesmo grau.
Grafos rotulado e valorado
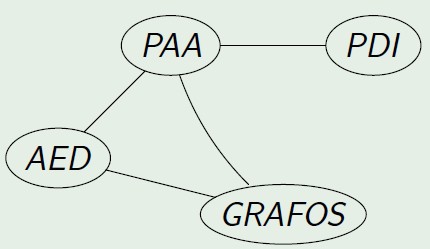
-> Grafo rotulado: um grafo G(V,A) é dito ser rotulado em vértices (ou arestas) quando a cada vértice (ou aresta) estiver associado um rótulo.
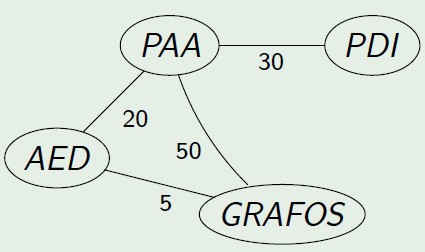
-> Grafo valorado: um grafo G(V,A) é dito ser valorado quando existe uma ou mais funções relacionando V e/ou A com um conjunto de números.




Comentários