
Conceitos em Grafos - Parte II
Ludmila Maciel Rocha de Souza

grafo completo
Um grafo G=(V,E) é completo se para cada par de vértices vi e vj existe uma aresta entre vi e vj . Em um grafo completo quaisquer dois vértices distintos são adjacentes (Kn).
Arestas no grafo completo - Seja Kn um grafo completo com n vértices. O número de arestas é:
Observações:
* (n - 1) é igual ao número de incidências nesse vértice.
* Em grafos não direcionados, para cada par de vértices existe uma aresta.
GRAFO CONEXO e bipartido
Grafo Conexo: Existe pelo menos um caminho entre todos os pares de vértices.
Grafo Bipartido: Um grafo é dito ser bipartido quando seu conjunto de vértices V puder ser particionado em dois subconjuntos V1 e V2, tais que toda aresta de G une um vértice de V1 a outro de V2.
GRAFO BIPARTIDO COMPLETO
Um grafo é dito ser bipartido completo quando seu conjunto de vértices V puder ser particionado em dois subconjuntos V1 e V2, tais que toda aresta de G une um vértice de V1 a outro de V2, e que todo vértice de V1 é adjacente a todo vértice de V2.
Arestas no grafo bipartido completo - Seja Kmn um grafo bipartido completo com n vértices em V1 e m
vértices em V2. O número de arestas é:
propriedade de grau
Grau: O número de arestas incidentes a um vértice vi é chamado de grau, d(vi ), do vértice i. A soma dos graus de todos os vértices de um grafo G é duas vezes o número de arestas de G.
TEOREMA - Vértice de grau ímpar: O número de vértices de grau ímpar em um grafo é par.
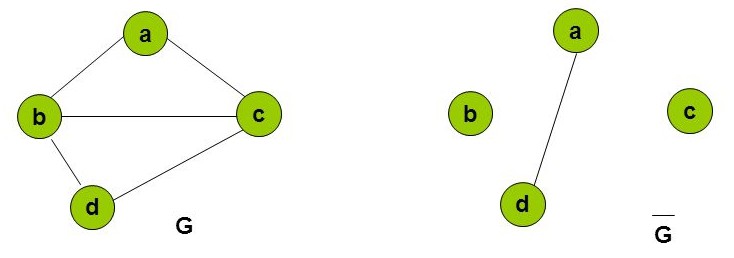
grafo complementar
O grafo complementar é o grafo nulo somado as arestas que faltam para o grafo em questão ser completo.
Definição formal:
* Seja G = (V, E) um grafo simples dirigido ou não-dirigido;
* O complemento de G, C(G), é um grafo formado da seguinte maneira:
- Os vértices de C(G) são todos os vértices de G;
- As arestas de C(G) são exatamente as arestas que faltam em G para formarmos um grafo completo.
subgrafos
- Um grafo g é dito ser um subgrafo de um grafo G se todos os vértices e todas as arestas de g estão em G;
- Observações:
* Todo grafo é subgrafo de si próprio; * O subgrafo de um subgrafo de G é subgrafo de G;
* Um vértice simples de G é um subgrafo de G; * Uma aresta simples de G (juntamente com suas extremidades) é subgrafo de G.
- Subgrafos disjuntos de arestas: dois (ou mais) subgrafos G1 e G2 de um grafo G são disjuntos de arestas se G1 e G2 não tiverem nenhuma aresta em comum.
- Subgrafos disjuntos de vértices: dois (ou mais) subgrafos G1 e G2 de um grafo G são disjuntos de vértices se G1 e G2 não tiverem nenhum vértice em comum.
Subgrafo induzido
Se G2 = (V2, A2) é um subgrafo de G1 = (V1, A1) e possui toda aresta (v,w) de G1 tal que ambos, v e w, estejam em V2, então G2 é o subgrafo induzido pelo subconjunto de vértices V2.
Exemplo:
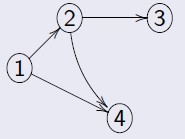
Grafo transposto
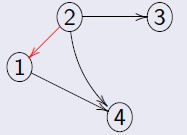
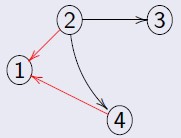
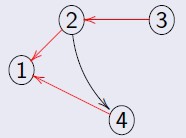
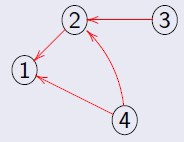
Dado um grafo direcionado G = (V, E), seu grafo transposto Gt = (V, E1), tal que E1 é o conjunto de arestas de G (E), com sentido oposto.
Abaixo o grafo transposto de um grafo direcionado:
| |

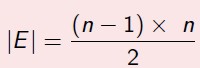




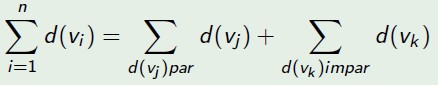

Comentários