Geovany Eugenio Silva de Araujo

 Vamos  utilizar a ferramenta Solver do Excel para solucionar problemas de programação linear

O exemplo a seguir é um problema de programação linear, que vai nos auxiliar a encontrar o uso otimizado das variáveis disponíveis no problema. O mesmo foi retirado do livro: Passos, Eduardo José Pedreira Franco. Programação Linear como instrumento de Pesquisa Operacional, Ed. Atlas, 2008. Pág. 37l.

Uma fábrica de Reboques produz reboques de luxo e reboques comerciais, e são utilizadas duas áreas produtivas. A área de montagem tem capacidade de produção de 5 reboques luxo e 2 reboques comercial dia, dispondo de 15 funcionários que trabalham durante 8 horas diárias. A área de pintura tem capacidade de produção de 4 reboques luxo e 1 reboque comercial dia, dispondo de 8 funcionários que trabalham 8 horas diárias. Ainda sabemos que o reboque luxo contribui com um lucro de R$360,00, enquanto o modelo comercial contribui com um lucro de R$285,00. Qual a produção máxima que a empresa deve ter para lhe proporcionar o maior lucro possível?

Em nossa tabela, a linha correspondente a área de montagem , vai receber sua capacidade de produção de acordo com o tipo de reboque a ser produzido. O mesmo acontece para a área de Pintura.

Note que na coluna Disponibilidade,para se obter o resultado em homens/horas, foi necessário multiplicar a quantidade de funcionários do respectivo setor pela quantidade de horas trabalhadas por dia.

Na linha correspondente ao Lucro, foi inserido os valores correspondentes do lucro que cada tipo de reboque contribui para com o faturamento da empresa.

Vamos definir alguns padrões:

• Os dados de entrada são os dados fornecidos pelo problema, como a função objetivo e as restrições.

• As células variáveis, como o próprio nome diz, vai mudar de acordo com o funcionamento do solver, ao invés de nomear as variáveis como x1 e y1, vamos definir essas células com nomes já pré-definidos pelo problema, afim de facilitar nosso entendimento.

_{​​​​​​​}

• As células de destino, vão armazenar o valor calculado da nossa função objetivo, já que o Solver possui a característica de alterar os valores das células variáveis afim de otimizar o valor da célula de destino.

• Dados de entrada :

-Nas Células C4:D5 vamos entrar com a capacidade de produção dos setores de acordo com o produto a ser fabricado.

-Nas células G4:G5 vamos inserir os dados a respeito da disponibilidade de cada setor, no nosso caso, a mão-de-obra dos funcionários, definida como horas trabalhadas.

-Nas Células C7 :D7 vamos entrar com os valores do lucro de cada produto respectivamente, que nada mais é que a nossa função objetivo.

• Unidades a serem produzidas:

- Nas células C11:D11 vamos iniciar com o valor 1. Estas são células variáveis, onde os valores das variáveis de decisão serão armazenadas. Estas células, através da resolução do SOLVER vão nos informar quanto deve ser produzido de cada produto a fim de atingir o resultado ótimo para o problema.

• Utilização dos recursos:

- Entre com a fórmula abaixo na célula E4:  (=SOMARPRODUTO(C4:D4;$C$11:D11) )

OBS: Aplique a fórmula nas outras restrições existentes, realizando as alterações que se fizerem necessárias.

Nota:

Esta fórmula calcula as unidades que cada setor consegue produzir, pela quantidade de produção inserida inicialmente.

A função somar produto multiplica cada valor do intervalo de células (C4:D4) pelos correspondentes valores nas células (C11:D11) e soma esses produtos, do mesmo modo que é feito na multiplicação de matrizes. 

Deve-se colocar o dólar nas células variáveis para fixá-las quando copiarmos a mesma fórmula para as outras restrições.

​​​​​​​

• Lucro Total:

-Entre com a fórmula abaixo na célula F7:  (=SOMARPRODUTO(C7:D7;C11:D11))

Nota:

Esta fórmula vai calcular o total de lucro de acordo com o número de unidades a serem produzidas presentes nas células variáveis.

Ao fim destes passos,você terá uma planilha semelhante a esta :

​

​​​​​​​

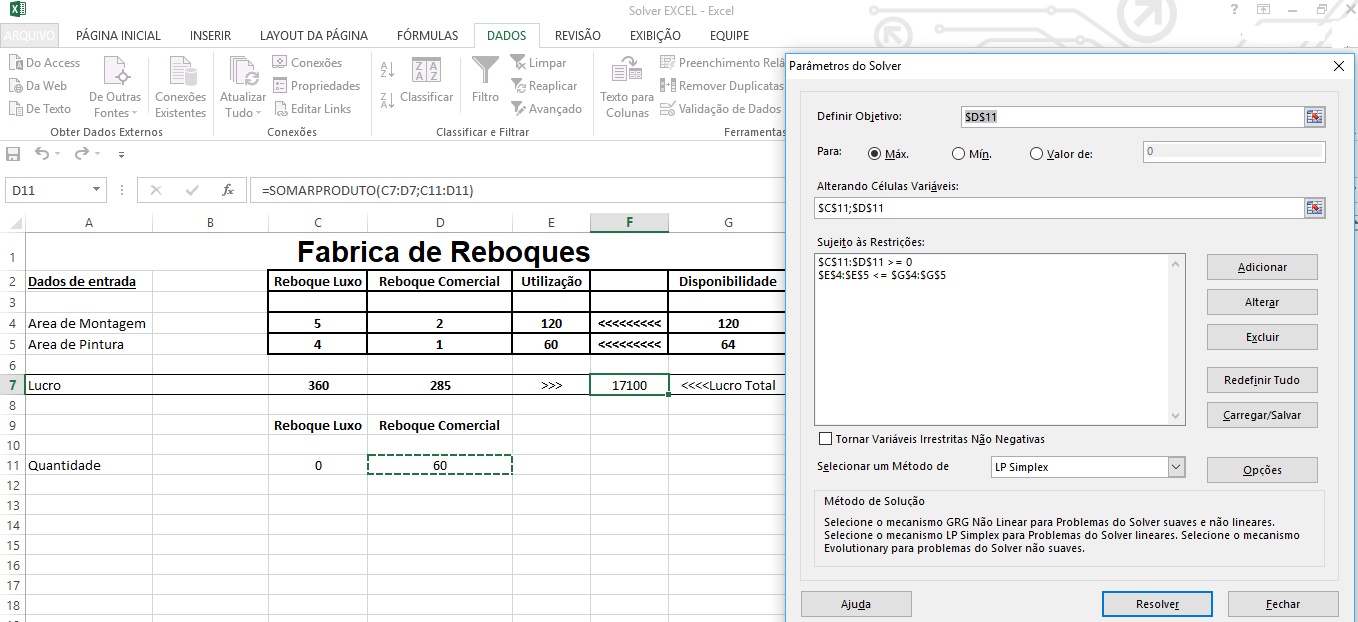
• Inicialmente vamos definir nossa célula de destino, onde irá receber o resultado da função objetivo, as células variáveis, e as restrições do problema, sem nos esquecer de incluir as restrições de não negatividade.

• Soluciona-se o problema por meio de ajustes nas células variáveis até que se encontre o valor máximo da célula de destino.

Encontre no menu a seguinte opção: 

• Dados  > Solver

- Selecione as células variáveis de acordo com a imagem abaixo.

-Adicione cada restrição, com a respectiva desigualdade. É necessário dar corretamente os endereços de cada desigualdade.

-Antes de resolver, clique em Selecionar um método de: "LP Simplex".

-Clique em resolver, o Solver mostrará nas células variáveis o valor ótimo das quantidades de reboques a serem fabricados, e o valor máximo do lucro.

Nota: Se a ferramenta não for encontrada, escolha o item suplementos (no menu ferramentas) e procure o Solver, clique na respectiva caixa de seleção.

​

Em alguns casos, para a solução ser condizente com a realidade, é necessário obtermos apenas valores inteiros em nossa solução.

Por exemplo, ao tentarmos otimizar o uso de mão-de-obra, tendo como medida pessoas, um valor decimal não é um valor coerente para ser aplicado, afinal, não podemos tirar “pedaços” de uma pessoa para atender nosso problema de acordo com a solução que foi fornecida.

Neste caso, devemos solicitar ao nosso solver, a solução inteira.

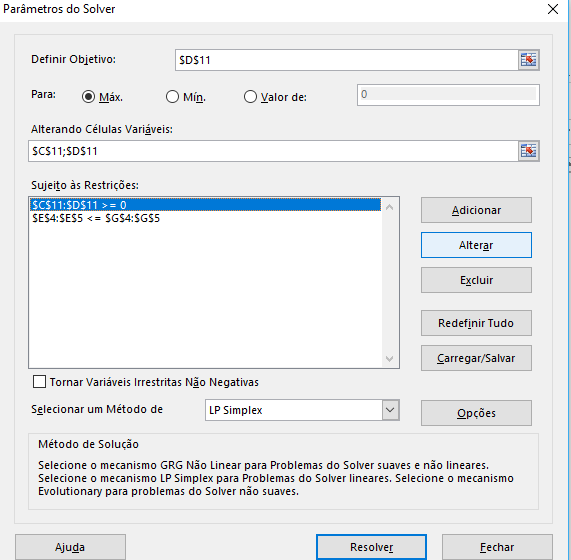
• Dados  > Solver

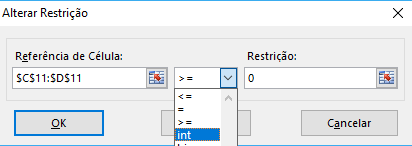
- Selecione suas células variáveis e clique em alterar.

​​​​​​​​

- Na opção para selecionar as desigualdades, selecione a opção int, ela vai resolver o problema de forma inteira, clique em OK.

​

- Clique em resolver.

Pronto! Sua solução está resolvida de forma inteira.

Definir e resolver um problema usando o Solver