
Tabelas verdade
Filipe Ferreira Bailon

você vai aprender
Proposições lógicas.
Conjunção, disjunção e negação.
Montar a tabela verdade.
pré-requisitos
Lápis e papel
Proposições lógicas
Tabela verdade é um tipo de tabela matemática usada em lógica para determinar se uma fórmula é válida, usamos para criá-las as proposições lógicas e conectivos lógicos.
Uma proposição lógica é um conjunto de palavras ou símbolos que exprimem sentido.
Uma proposição simples é aquela que não contém outra proposição integrante dentro de si.
Exemplos:
p: Pedro é estudante
q: O número 25 é um quadrado perfeito
r: x ∈ A
Uma proposição composta é aquela feita pela composição de uma ou mais proposições.
Exemplos:
p: Pedro é estudante e Maria é professora.
q: Se o número 25 é um quadrado perfeito então a raiz quadrada de 25 é um número inteiro.
r: x ∈ A ou x ∈ B
conectivos lógicos
Conjunção, conectivo e:
Exemplo: Paulo é dentisa e Julio é médico.
Representemos da seguinte forma: A ∧ B, sendo A = Paulo é dentista e B = Júlio é jogador de futebol.
Uma proposição conjuntiva (e) só terá seu valor verdadeiro se ambas afirmativas forem verdadeiras, logo, nessa proposição composta acima ambos tem que desempenhar tais funções para haver um valor logicos verdadeiro.
Disjunção, conectivo ou:
Exemplo: Irei à praia ou irei ao cinema.
Representemos da seguinte forma: A ∧ B, sendo A = Irei à praia e B = Irei ao cinema.
Uma proposição disjuntiva (ou) só tera seu valor falso se ambas as afirmativas forem falsas. De outro modo será considerada verdadeira. Na proposição acima ou irei a um lugar ou irei a outro, mesmo não indo a um desses lugares eu posso ir a outro, só não posso deixar de ir a um deles.
Negação: ~A
Exemplo: A = A bicleta é azul
~A = A bicicleta não é azul.
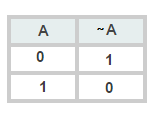
Quando a bicicleta for azul (p), sua negação será falsa (~p). Se a afirmação for falsa, a negação será verdadeira.
criando a tabela verdade
Para criar uma tabela verdade colocamos todas as possibilidades de verdadeiro ou falso para os argumentos das proposições.
Na lógica classica trabalhamos com o princípio do terceiro excluído, ou seja, dada uma proposição qualquer, os únicos valores que ela pode assumir é Verdadeiro(1) ou Falso(0).
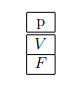
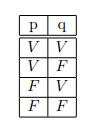
Se temos uma proposição simples, sua tabela verdade seria assim:
Com duas proposições simples temos:
usando os conectivos nas proposições
Exemplo:
p = Paulo é dentista.
q = Julio é medico.
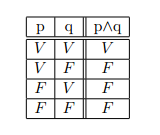
Paulo é dentista e julio é médico.
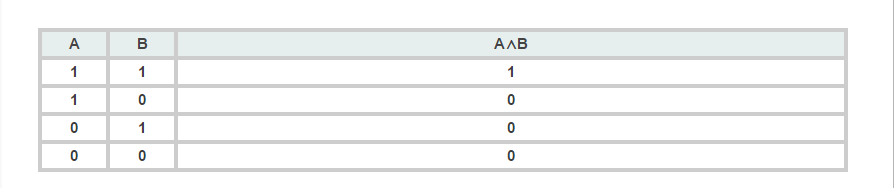
O resultado dessa conjunção só pode ser verdadeiro se p e q forem verdadeiros:
Exemplo:
p = Irei à praia.
q = Irei ao cinema.
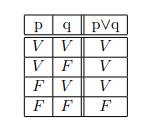
Irei à praia ou ireia ao cinema
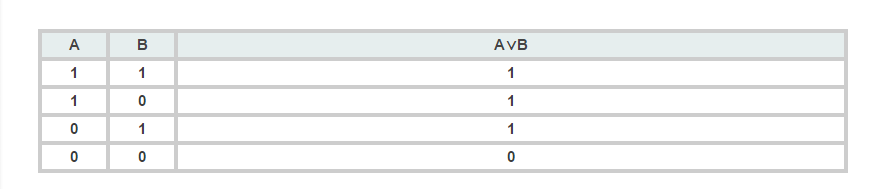
O resultado dessa disjunçao so pode ser falso se p e q forem falsos, ou seja, não foi a lugar algum:
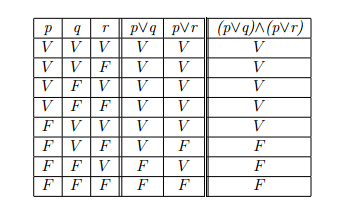
Suponhamos o seguinte argumento: (p ou q) e (p ou r)
Faremos por etapa e o argumento será verdadeiro ou falso nas seguintes situações:
Para simplificar as tabelas e se aprofundar mais você pode estudar álgebra booleana e mapas de Karnaugh.
links úteis
Este tutorial foi adaptado do tutorial "Criando tabelas verdade" desenvolvido por Erick Moreira.
Comentários